ダイクストラ法

解説/アルゴリズム

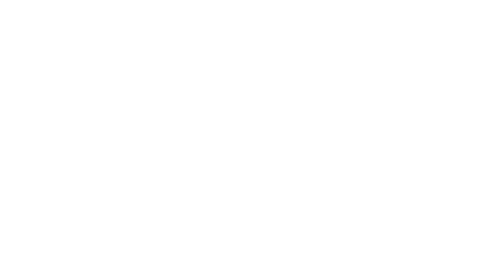
辺に重みが付いているグラフのことを重み付きグラフと呼び、上記のような形となる。

重みは頂点間の移動距離や時間を表しており、上記の ABCD の各頂点は駅名、辺の数字は駅間の移動時間だと考えてみる。

たとえば A 駅から D 駅までを最短の時間で移動したい場合、A 駅から D 駅へと直接移動すると 20 分かかるが、A 駅->B 駅->C 駅->D 駅と移動すると 18 分で済む。

このように重み付きグラフの場合、移動する頂点の数が短かければ最短経路になるとは限らない。

これから説明するダイクストラ法は重み付きグラフにおいて最短経路を求めるアルゴリズムとなる。

ただし辺の重みに負数が含まれる場合はダイクストラ法を利用することはできない。

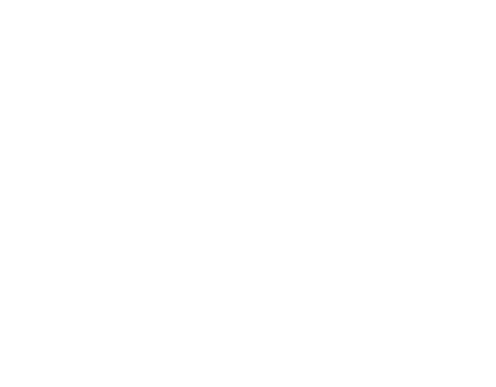
新たに重み付きグラフを用意して、頂点 A が開始地点だとする。

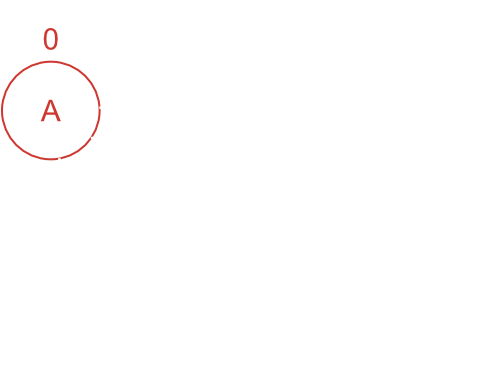
A から開始をしているので、当然ながら A までの最短距離は 0 になる。

画像ではわかりやすいように、確定した頂点の付近にその頂点までの最短距離を書き、頂点の色を赤に変更している。

確定頂点: [A]
A までの最短距離: 0 / ルート: [A] (確定)

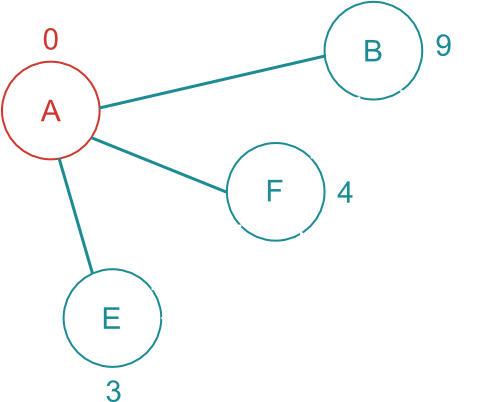
最短経路が確定した A に繋がっている頂点に A からの距離を書き加えておく。

（A-B / A-F / A-E 間の距離を、各頂点に保持しておく。）

A に繋がっているこれらの頂点は次に最短経路が確定するかもしれない未確定頂点。

画像ではわかりやすいように、未確定頂点の色とルートを青色に変更している。

未確定頂点: [B, F, E]
確定頂点: [A]
A までの最短距離: 0 / ルート: [A] (確定)
B までの最短距離: 9 / ルート: [A-B] (未確定)
F までの最短距離: 4 / ルート: [A-F] (未確定)
E までの最短距離: 3 / ルート: [A-E] (未確定)

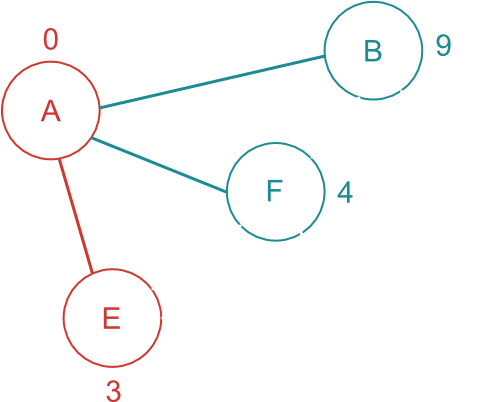
開始地点から一番短い経路で繋がっている未確定頂点を探す。

A-B / A-F / A-E の中では、A-E 間の距離が一番短いので、E まで移動するには、A-E 間が最短であることが確定する。

何故かというと最短経路が確定している A に繋がっている頂点の中で、一番短い経路が A-E なので、他の経路、たとえば A-F や A-B から E の方に周りこんだルートが A-E より小さくなることはありえないから。

未確定頂点: [B, F]
確定頂点: [A, E]
A までの最短距離: 0 [A] (確定)
B までの最短距離: 9 [A-B] (未確定)
F までの最短距離: 4 [A-F] (未確定)
E までの最短距離: 3 [A-E] (確定)

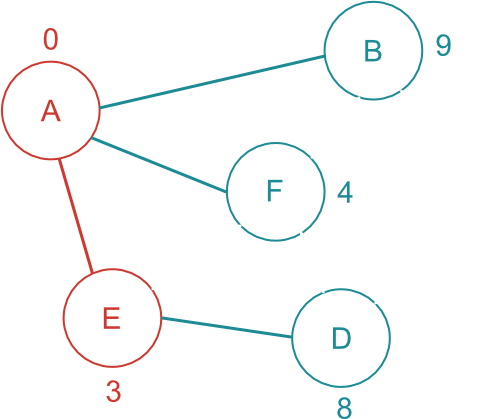
最短経路が確定した E に繋がっている頂点である D と F に注目する。

D は新しく繋がった未確定頂点。

それに加え、E には 3 という開始地点からの距離が保持されているが、それに E-D 間の距離を足した 8 を D に書き込んでおく。

つまり、まだ未確定だが、開始地点からの最短距離を暫定的に頂点に書き込んでおく。

F はすでに候補になっている頂点なので、開始地点から F までの暫定的な最短距離 4 が書き込まれている。

それがさらに短くできるならば更新を行う。

A-E-F の距離は 5 だが、もともと存在していた A-F の経路の方が短いので、F までの暫定的な最短距離の情報は更新をしない。

今のところ、未確定だが F までの最短経路は A-F のままとなる。

未確定頂点: [B, D, F]
確定頂点: [A, E]
A までの最短距離: 0 [A] (確定)
B までの最短距離: 9 [A-B] (未確定)
D までの最短距離: 8 [A-E-D] (未確定)
F までの最短距離: 4 [A-F] (未確定)
E までの最短距離: 3 [A-E] (確定)

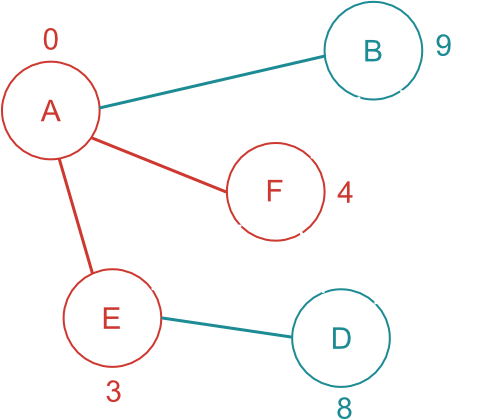
開始地点から一番短い経路で繋がっている未確定頂点を探す。

A-B / A-F / A-E-D の中では、A-F 間の距離が一番短いので、F まで移動するには、A-F 間が最短であることが確定する。

未確定頂点: [B, D]
確定頂点: [A, E, F]
A までの最短距離: 0 [A] (確定)
B までの最短距離: 9 [A-B] (未確定)
D までの最短距離: 8 [A-E-D] (未確定)
F までの最短距離: 4 [A-F] (確定)
E までの最短距離: 3 [A-E] (確定)

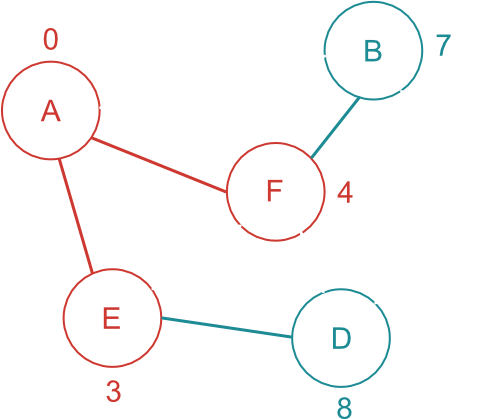
最短経路が確定した F に繋がっている頂点である B と D に注目する。

B と D に書き込まれている最短距離より、A-F から通る距離の方が短ければ、情報を更新する。

B の場合、A-B の距離 9 より A-F-B の距離 7 の方が短いので、B 頂点までの最短経路が 7 に更新される。

D の場合、A-E-D の距離 8 より A-F-D の距離 9 の方が長いので、D 頂点までの最短経路は 8 のままになる。

未確定頂点: [B, D]
確定頂点: [A, E, F]
A までの最短距離: 0 [A] (確定)
B までの最短距離: 7 [A-F-B] (未確定)
D までの最短距離: 8 [A-E-D] (未確定)
F までの最短距離: 4 [A-F] (確定)
E までの最短距離: 3 [A-E] (確定)

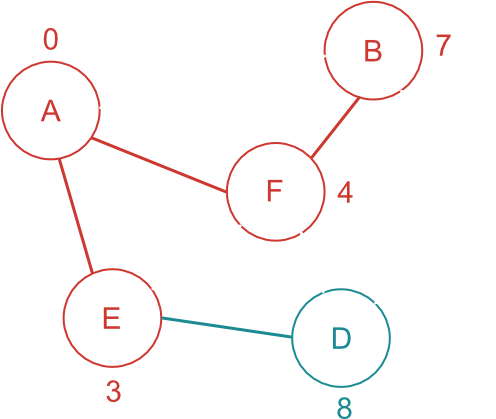
開始地点から一番短い経路で繋がっている未確定頂点を探す。

A-B / A-E-D の中では、A-B 間の距離が一番短いので、B まで移動するには、A-B 間が最短であることが確定する。

未確定頂点: [D]
確定頂点: [A, B, E, F]
A までの最短距離: 0 [A] (確定)
B までの最短距離: 7 [A-F-B] (確定)
D までの最短距離: 8 [A-E-D] (未確定)
F までの最短距離: 4 [A-F] (確定)
E までの最短距離: 3 [A-E] (確定)

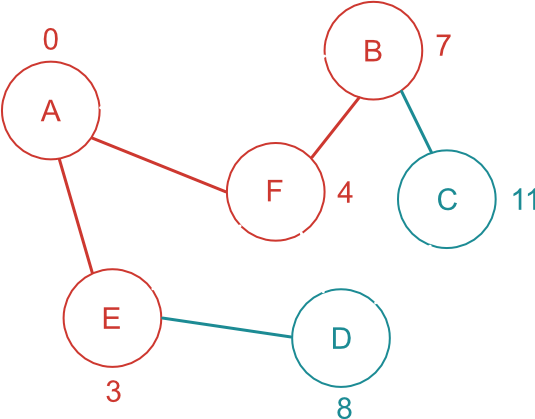
最短経路が確定した B に繋がっている頂点である C に注目する。

C は新しく繋がった未確定頂点。

B までの最短距離 7 に B-C 間の距離を足した 11 を C に書き込んでおく。

未確定頂点: [C, D]
確定頂点: [A, B, E, F]
A までの最短距離: 0 [A] (確定)
B までの最短距離: 7 [A-F-B] (確定)
C までの最短距離: 11 [A-F-B-C] (未確定)
D までの最短距離: 8 [A-E-D] (未確定)
F までの最短距離: 4 [A-F] (確定)
E までの最短距離: 3 [A-E] (確定)

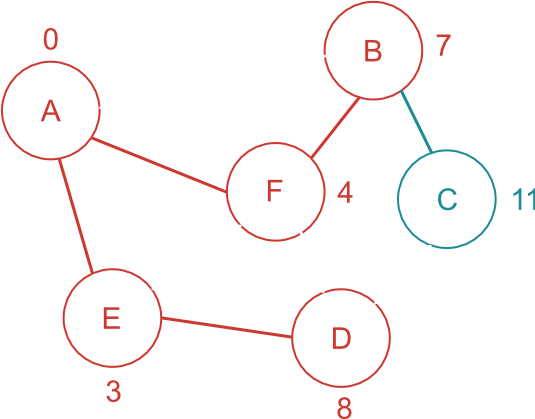
開始地点から一番短い経路で繋がっている未確定頂点を探す。

A-F-B-C / A-E-D の中では、A-E-D 間の距離が一番短いので、D まで移動するには、A-E-D 間が最短であることが確定する。

未確定頂点: [C]
確定頂点: [A, B, D, E, F]
A までの最短距離: 0 [A] (確定)
B までの最短距離: 7 [A-F-B] (確定)
C までの最短距離: 11 [A-F-B-C] (未確定)
D までの最短距離: 8 [A-E-D] (確定)
F までの最短距離: 4 [A-F] (確定)
E までの最短距離: 3 [A-E] (確定)

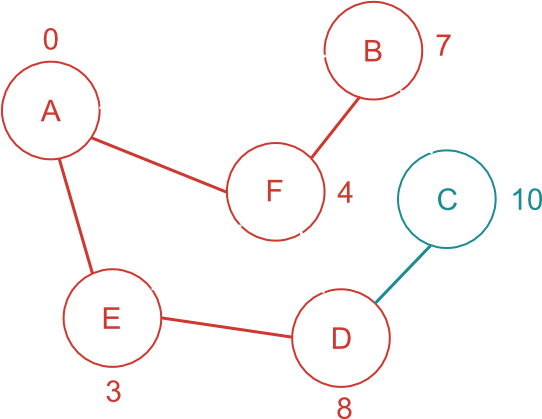
最短経路が確定した D に繋がっている頂点である C に注目する。

C に書き込まれている最短距離より、A-E-D から通る距離の方が短ければ、情報を更新する。

C の場合、A-F-B-C の距離 11 より A-E-D-C の距離 10 の方が短いので、C 頂点までの最短経路が 10 に更新される。

未確定頂点: [C]
確定頂点: [A, B, D, E, F]
A までの最短距離: 0 [A] (確定)
B までの最短距離: 7 [A-F-B] (確定)
C までの最短距離: 10 [A-E-D-C] (未確定)
D までの最短距離: 8 [A-E-D] (確定)
F までの最短距離: 4 [A-F] (確定)
E までの最短距離: 3 [A-E] (確定)

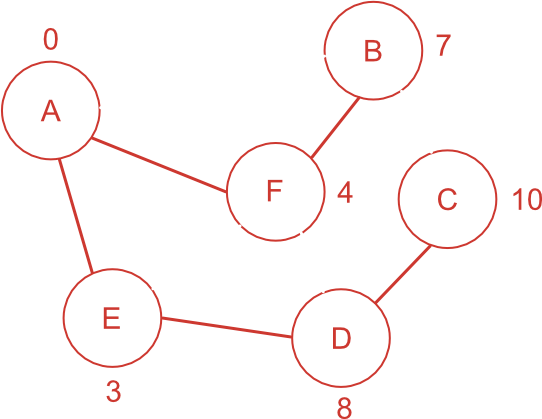
開始地点から一番短い経路で繋がっている未確定頂点を探す。未確定頂点は C しか残っていないので、C まで移動するには、A-E-D-C 間が最短であることが確定する。

未確定頂点: []
確定頂点: [A, B, C, D, E, F]
A までの最短距離: 0 [A] (確定)
B までの最短距離: 7 [A-F-B] (確定)
C までの最短距離: 10 [A-E-D-C] (確定)
D までの最短距離: 8 [A-E-D] (確定)
F までの最短距離: 4 [A-F] (確定)
E までの最短距離: 3 [A-E] (確定)

コード例

#include <bits/stdc++.h>

using namespace std;
using ll = long long;
using P = pair<ll, ll>;

struct Edge {
  int to;
  ll cost;
};

int main() {
  int n = 4;  // 頂点数
  int s = 0;  // 始点

  vector<vector<Edge>> edge(n);
  // 辺の登録。例えば一番上は頂点0から頂点1まで移動するのにコストが1かかることを表している
  edge[0].push_back({1, 1});
  edge[0].push_back({2, 4});
  edge[1].push_back({2, 2});
  edge[2].push_back({3, 1});
  edge[1].push_back({3, 5});

  // 始点から各頂点までの移動総コスト
  // 始点は0、それ以外の頂点は入ることがあり得ない大きい値にしておく
  int INF = 1000000000;
  vector<int> dist(n, INF);
  dist[s] = 0;

  // 未確定の頂点の中から始点からの移動総コストが最小のものを高速に取り出すため、
  // 優先度付きキューを利用する
  // pair{頂点までの暫定コスト, 頂点}
  priority_queue<P, vector<P>, greater<P>> pq;
  // 始点と始点までのコスト0を入れておく
  pq.push({0, s});

  // 優先度付きキューが空になるまでループ
  while (!pq.empty()) {
    // 未確定の頂点の中から始点からの移動総コストが最小のものを取り出す
    // この時点で、始点から取り出した頂点までの最短コストが確定する
    P p = pq.top();
    pq.pop();

    // 具体的な名前に変更
    ll cost = p.first;
    int cur = p.second;

    // 既にcostより小さい値で確定されているのでスキップ
    if (dist[cur] < cost) {
      continue;
    }

    // 頂点に繋がっている各頂点を走査
    for (auto e : edge[cur]) {
      // 計算したコストが暫定コストより小さければ更新。
      // 次の頂点を優先度付きキューに追加する
      ll new_cost = dist[cur] + e.cost;
      if (new_cost < dist[e.to]) {
        dist[e.to] = new_cost;
        pq.push({new_cost, e.to});
      }
    }
  }

  for (auto x : dist) {
    cout << x << endl;
  }
}

キューの仕様上、同じ頂点を追加した際、別々なものとして扱うので、確定した頂点なのにまたキューからその頂点が出てくるということがある。

その場合、無駄な走査を行わないように、 if (dist[cur] < cost) ならスキップを行うという処理を入れるのがポイントとなる。

計算量

優先度付きキュー（ヒープ）を用いる場合、計算量は $O(|E|log|V|)$ になる。

みさご解体新書

ダイクストラ法

解説/アルゴリズム

コード例

計算量